Journal of Statistical Software
- August 2013, Volume 54, Issue 2.
- http://www.jstatsoft.org/
adabag: An R Package for Classi cation
with Boosting and Bagging
- Esteban Alfaro
University of
Castilla-La Mancha - Mat as G amez
University of
Castilla-La Mancha - Noelia Garc a
University of
Castilla-La Mancha
개요 (Abstract)
부스팅과 배깅(Boosting and bagging)은 분류를 위한 앙상블 방법으로 폭넓게 사용되는 2가지이다. 그들의 공동의 목표는 무작위 추측보다 약간 더 좋은 단일 분류기를 결합하여 분류기의 정확성을 향상하기 위함이다. 부스팅 알고리즘의 가족 중에서, AdaBoost(adaptive boosting)가 가장 알려졌다, 비록 그것은 단지 이분법적인 작업에서 안정적이지만. AdaBoost.M1 와 SAMME (stagewise additive modeling using a multi-class exponential loss function)는 쉬운 2가지이다 그리고 2개 또는 더 많은 분류의 일반적인 경우로 자연스럽게 확장된다. 이 논문에서 adabag R 패키지가 소개 되었다. 이 버전은 기본 분류기로 분류 트리를 가지고 AdaBoost.M1, SAMME 그리고 배깅 알고리즘(bagging algorithms)을 구현했다. 일단 앙상블을 훈련 하고, 그들은 새로운 표본의 분류를 예측하기 위해 사용된다. 게다가, 앙상블이 성장에 따라 에러의 전개(the evolution of the error)가 분석되고 그리고 앙상블은 정리된다. 추가로, 분류 예측에서 한계(margin)와 관측에서 각 분류의 가능이 계산 된다. 마지막으로 분류 학문에서 몇몇 고전적인 예가 이 패키지의 사용을 설명하기 위해 보여진다.
Keywords: AdaBoost.M1, SAMME, bagging, R program, classi cation, classi cation trees.
Contents
1 소개(Introduction)
지난 수십년 동안, 트리 구축을 기본으로한 몇몇의 새로운 앙상블(ensembles) 분류 방법이 개발되어 왔다. 이 장에서, R 의 패키지 adabag (R Core Team 2013)이 설명된다, 트리의 앙상블(ensembles)을 위한 가장 유명한 방법 2가지를 구현함: boosting 과 bagging. 이 두 앙상블 간 주요 차이는 boosting이 연속해서 그것의 기본 분류기를 구축하고, 각 기본 분류기를 생성하기 위해 훈련 표본 전체에서 분포를 업데이트 하지만, bagging (Breiman 1996)은 훈련 집합의 부트스트랩 복제(bootstrap replicates)에서 생성된 개별 분류기를 결합한다. Boosting은 알고리즘 군이다 그리고 그들 둘은 여기서 구현되었다: AdaBoost.M1 (Freund and Schapire 1996) 그리고 SAMME (Zhu, Zou, Rosset, and Hastie 2009). 우리가 아는 한, SAMME 알고리즘은 어떤 다른 R 패키지에서 이용 가능하지 않다.
패키지 adabag 3.2, Comprehesive R Archive Network http://CRAN.R-project.org/package=adabag 에서 이용 가능, 트리에서, boosting 함수의 경우에서, 이 트리의 가중치, 변수에서 주어진 Gini 계수를 얻기 위해 사용하는 예측자 변수의 연관 중요도의 측정치의 변경한 adabag이 최신 업데이트이다. 이런 목적으로 caret 패키지(Kuhn 2008, 2012)의 varImp 함수가 각 트리에서 변수의 지니 계수(Gini index)를 얻기기 위해 사용되었다.
이전에, 4개의 중요한 새로운 특징을 소개한 버전 3.0: AdaBoost-SAMME가 다루어졌다; 새로운 함수 errorevol는 반복의 수에 따라 앙상블 에러를 보여준다; 앙상블은 predict 함수와 상응하는 옵션 newmfinal를 사용하여 가지치기를 한다; 모든 관측에서 각 분류의 후부의 확률이 얻어진다. 추가적으로, 버전 2.0에는 분류기를 위한 마진을 계산하기 위해 함수 margins이 포함되었다.
2006년에 이 패키지의 첫번째 버전이므로, 그것은 다음과 같은 매우 다른 과학적 영역의 몇몇의 분류 작업에서 사용되었다; 경제학 그리고 금융(재정) (Alfaro, Garc a, G amez, and Elizondo 2008; Chrzanowska, Alfaro, and Witkowska 2009; De Bock and Van den Poel 2011), 자동화된 컨텐츠 분석 (Stewart and Zhukov 2009), 품질 관리에서 하나의 out-of-control의 해석 (Alfaro, Alfaro, G amez, and Garc a 2009), 기계 학습의 발전 (advances in machine learning) (De Bock, Coussement, and Van den Poel 2010; Krempl and Hofer 2008). 게다가, adabag은 R 패키지 digeR에서 사용되었다 (Fan, Murphy, and Watson 2012) 그리고 적어도 2개의 R 메뉴얼에서 (Maindonald and Braun 2010; Torgo 2010).
adabag과 별도로, 지금까지 부스팅 모델을 처리하는 몇개의 R 패키지가 있다. 그중에서도, 가정 넓게 사용되는 것은 ada (Culp, Johnson, and Michailidis 2012), gbm (Ridgeway 2013) 그리고 mboost (Buhlmann and Hothorn 2007; Hothorn et al. 2013) 이다. 그들은 실제로 유용하고 그리고 잘 문서화된 패키지이다. 어쨌든, 그것은 그들이 회귀와 이분법적 분류(dichotomous classification)를 위한 부스팅(boosting)에 더 초점이 맞춰졌다. 부스팅(boosting) 패키지의 더 상세한 개정(revision)을 위해 흥미로운 CRAN 작업보기를 보라: "Machine Learning & Statistical Learning" maintained by Hothorn (2013).
문서는 다음과 같이 구성되었다: 2 절에서 앙상블 알고리즘 AdaBoost.M1, SAMME 그리고 배깅의 요약된 설명을 하고, 3 절은 패키지 함수를 설명한다. 여기에는 8개의 함수가 있다, 그들 중 3개는 각 앙상블 군을 지정하고 그리고 그들 중 2개는 모든 방법에서 공통이다. 추가적으로, 모든 함수는 잘 알려진 분류 문제를 통해서 설명했다. 그러므로 4 절은 둘 보다 더 복잡한 분류 데이터 셋으로 패키지의 작업에서 심도있는 내적 가치를 제공하기 위해 할애했다. 마지막으로, 어떤 마지막 결론은 5절에서 이끌어 낸다.
2. 알고리즘(Algorithms)
이 절에는 부스팅(boosting) 그리고 배깅(bagging) 알고리즘의 요약된 설명이 주어진다. 그들의 공통의 목표은 앙상블의 정확성을 향상시키기 위함이다, 가능한 같고 다른 하나의 분류기를 결합. 두 경우에, 이질(이종, heterogeneity)은 개별적인 다른 분류기로 생성된 경우에 훈련 집합을 수정하여 소개되었다. 어쨌든, 각 부스팅 반복의 기본 분류기는 모두 가중치 업데이트 과정을 통해 이전의 하나에 의존하다. 추가적으로, 최종 부스팅 앙상블(final boosting ensemble)은 가중된 중요도 선택을 사용한다 그런데 배깅(bagging)은 단순한 중요도 선택을 사용한다.
2.1. Boosting
부스팅(boosting)은 그것의 정확도를 향상하기 위해 분류기를 최대로 사용하게 만드는 방법이다. 분류기의 메서드는 훈련 집합에서 극도로 정확한 분류기를 만들기 위해 서브루틴(subroutine)으로 이용되어 진다. 부스팅(boosting)은 훈련 집합에서 반복되는 분류 시스템이다, 그러나 각 단계에서 학습 처리는 적응 가중치(adaptive weights)를 사용하여 같은 집합의 다른 표본에 초점을 맞춘다, 훈련 집합에서 매우 정확한 분류기. 최종 분류기는 그러므로 데이터 셋에 높은 정밀도에 보통은 도달한다, 다양한 저자가 이론적 및 실증적으로 보여 주었다 (Ban eld, Hall, Bowyer, and Kegelmeyer 2007; Bauer and Kohavi 1999; Dietterich 2000; Freund and Schapire 1997).
부스팅(boosting) 알고리즘에는 몇가지 다른 버전이 있지만 (Schapire and Freund 2012; Friedman, Hastie, and Tibshirani 2000), 최고로 알려진 것은 AdaBoost (Freund and Schapire 1996) 이다. 어쨌든, 그것은 이진 분류 문제에서만 유일하게 적용할 수 있다. 다중 분류 문제를 위한 부스팅 알고리즘 사이에서 (Mukherjee and Schapire 2011), AdaBoost의 가장 단순하고 자연스러운 확장에서 둘이 선택되었다, AdaBoost.M1 그리고 SAMME 라 불림.
첫번째로 AdaBoost.M1 알고리즘은 다음과 같이 설명할 수 있다. 주어진 훈련 집합 Tn = {(x1, y1), ... , (xi, yi), ... , (xn, yn)} 이고 yi는 1, 2, ..., k 값을 가진다. 가중치 ωb(i) 는 각 관측값 xi 할당되고 그리고 초기값은 1/n 으로 놓는다. 이 값은 각 단계 후에 수정될 것이다. 기본 분류기는, Cb(xi), 새로운 훈련 집합 ( Tb)에서 만들어진다. 이 분류기의 에러는 eb로 표현되고 그리고 다음과 같이 계산된다.
eb = Σi=1 n ωb(i) Ι (Cb(xi) ≠ yi) (1)
I(·)은 만약 내부 식이 참이면 1 그리고 그렇지 않으면 0 인 지시 함수(indicator function)인 경우에.
b-번째 반복에서 분류기의 에러에서, 상수 αb 는 계산되고 그리고 가중치를 수정하기 위해 사용된다. 특히, Freund 와 Schapire에 따라, αb = ln ((1 - eb)/eb). 어쨌든 Breiman (Breiman 1998)은 αb = 1/2 ln((1 - eb)/eb) 를 사용했다. 항상, (b + 1)-번째 반복을 위한 새로운 가중치는 다음이 될 것이다.
ωb+1(i) =
ωb(i)
exp(αb I (Cb(xi) ≠ yi))
(2)
나중에, 계산된 가중치는 하나로 합하여 정규화 된다. 따라서, 잘못 분류된 관측의 가중치는 증가되고, 그리고 올바르게 분류된 가중치는 감소한다, 가장 어려운 예에 초점을 맞추기 위해 다음 반복에서 생성될 분류기를 강제함. 게다가, 가중치 갱신의 차이는 하나의 분류기가 낮을 때 더 크다 왜냐하면 만약 분류기가 높은 정확도에 도달하고 그러면 몇몇의 오류를 더 중요하게 여긴다. 이런 까닭으로, 알파 상수는 각 단계에서 만들어진 에러 함수로써 계산된 학습 비로 해석되어 진다. 게다가, 이 상수는 더 낮은 에러를 만드는 개별적인 분류기가 더 중요한 최종 결정 규칙에서 사용되어 진다.
| 1. | ωb(i) = 1/n, i = 1, 2, ... n 을 가지고 시작하라. |
| 2. |
b = 1, 2, ..., B 로 반복해라
|
| 3. | 최종 분류기 Cf(xi) = arg maxj∈Y Σb=1B αb I (Cb(xi) = j) 를 출력해라 |
Table 1: AdaBoost.M1 algorithm.
| 1. | ωb(i) = 1/n, i = 1, 2, ... n 을 가지고 시작하라. |
| 2. |
b = 1, 2, ..., B 로 반복해라
|
| 3. | 최종 분류기 Cf(xi) = arg maxj∈Y Σb=1B αb I (Cb(xi) = j) 를 출력해라 |
Table 2: SAMME algorithm
이 과정은 b = 1, 2, ... , B 의 모든 단계를 반복한다. 최종적으로 앙상블 분류기는 계산한다, 각 분류를 위해, 그것의 가중된 합을 선택한다. 그러므로, 가장 많이 선택되는 분류는 할당된다. 특히,
Cf(xi) =
arg maxj∈Y Σb=1B
αb I (Cb(xi) = j)
(3)
Table 1는 완전한 AdaBoost.M1 의사 코드(pseudocode)를 보여준다.
SAMME는, 여기서 구현된 두번째 부스팅 알고리즘, Table 2에 요약 되었다. 그것은 이 알고리즘과 AdaBoost.M1 사이의 단지 다른 것은 알파 상수가 계산되는 곳에서 방법임을 다룰 가치가 있다, 왜냐하면 분류의 수는 이 경우에 고려되기 때문이다. 수정을 위해, SAMME 알고리즘은 알파가 양수가 되고 가중치 갱신이 올바른 방향을 따르도록 하기 위한 명령으로 1 - eb > 1/k 가 단지 필요할 뿐이다. 그것은 말한다, 각각의 약한 분류기의 정확도는 1/2 대신에 무작의 추측 (1/k) 보다 더 좋아야 될 것이다, 다중 분류 하나를 위한 다양한 요구를 제외한 2개의 분류 경우를 위해 적당한 요구가 됨.
2.2. Bagging
배깅(bagging)은 부트스트래핑과 집계(bootstrapping and aggregating)를 결합하는 방법이다(Table 3). 만약 부트스트랩(bootstrap)이 전통적인 하나 보다 더 정확하고 강건하게 데이터 분산 파라메터를 추정한다면, 그러면 비슷한 방법으로 달성하기 위해 사용할 수 있다, 그들을 결합한 후에, 더 나은 특징을 가지는 분류기.
| 1. |
b = 1, 2, ..., B 로 반복해라
|
| 2. | 최종 결정 규칙 Cf(xi) = arg maxj∈Y Σb=1B I(Cb(xi) = j) 에서 가장 중요한 선택으로 (가장 자주 예측되는 분류) 기본 분류기 Cb(xi) = {1, 2, .... , B} 를 결합해라. |
Table 3: Bagging algorithm
훈련 집합 (Tn)을 기반으로, B 부트스트랩(bootstrap) 표본 (Tb) 가 얻어진다, b = 1, 2, ..., B 인 경우. 이러한 부트스트랩(bootstrap)은 원본 집합 (이 경우에 n) 보다는 같은 요소의 수를 교체하여 얻어진다(원본: These bootstrap samples are obtained by drawing with replacement the same number of elements than the original set (n in this case).). 이런 부트스트랩(bootstrap) 표본 일부에서, 관측 잡음은 제거 되거가 또는 적어도 감소될 것이다, (비-잡음 표본 보다는 잡음의 낮을 확률이므로) 그래서 이러한 집합에서 생성된 분류기는 원본 집합에서 생성된 분류기 보다 더 나은 가동을 가질 것이다. 그러므로, 배깅(bagging)은 훈련 집합에 잡음 관측이 있을 때 더 나은 분류기를 생성하기에 실제로 유용하게 될 것이다.
앙상블(ensemble)은 최종 분류기를 생성하기 위해 사용된 단일 분류기 보다 일반적으로 더 나은 결과를 나타내다. 이것은 분류기의 결합은 또한 최종 앙상블(ensemble)에서 각각 하나의 이점을 결합하는 것으로 이해가 될 수 있다.
2.3. 여분 (The margin)
부스팅 문헌(boosting literature)에서, 마진(margin)의 개념은 (Schapire, Freund, Bartlett, and Lee 1998) 중요하다. 객체의 마진은 분류의 확실성에 직관적으로 연관이 있고 그리고 올바른 분류(등급, class) 지지도 및 잘못된 분류의 최대 지지도 사이의 차이(difference)로 계산 된다. k 분류에서, 표본 xi의 마진은 최종 앙상블에서 모든 분류 j 에서 선택을 사용하여 계산된다, 차이 분류 (difference classes) 또든 사후 확률 (posterior probabilities) μj (xi), j = 1, 2, ..., k 의 지지도로 알려짐:
m (xi) =
μc(xi) -
maxj≠c μj (xi)
(4)
c는 xi의 올바른 분류(correct class)이고 그리고 Σj=1k μj(xi) = 1 인 경우. 모든 잘못 분류된 표본은 그러므로 음수의 마진을 가질 것이고 그리고 이것들이 올바르게 분류된 하나는 양수의 마진을 가질 것이다. 높은 신뢰도를 가지는 올바르게 분류된 관측은 1에 가깝게 될 것이다. 다른 한편으로는, 불확실한 분류를 가지는 표본은 작은 마진을 가질 것이다, 즉 말하자면, 마진은 0 에 가깝게 된다. 작은 마진은 할당된 분류에 불안정한 징후이기 때문에, 같은 표본은 비슷한 분류기에서 다른 분류로 할당될 것이다. 시각화 용도를 위해, Kuncheva (2004)는 주어진 데이터 셋을 위한 마진의 누적 분포를 보여주는 마진 분포 그래프를 사용했다. x-축은 마진 (m) 그리고 y-축은 마진이 m 과 같거나 작은 경우의 포인트의 수 이다. 이상적으로, 모든 포인트는 올바르게 분류될것이다 그래서 모든 마진은 양수이다. 만약 모든 폰인트가 올바르게 분류된다면 그리고 최대 가능 확실성 (the maximum possible certainty) 을 가진다면, 누적 그래프는 m = 1 인 하나의 수직선이 될 것이다.
3. Functions
이 절에서, R의 adabag 패키지의 함수가 설명된다. 전에 언급한 바와 같이, 그것은 분류와 회귀 트리를 가지는 AdaBoost.M1, SAMME 그리고 bagging 구현한다, (CART, Breiman, Friedman, Olshenn, and Stone 1984) rpart 패키지를 사용하는 기본 분류기로써 (Therneau, Atkinson, and Ripley 2013). 여기에서 boosted 또는 bagged 트리가 사용되었다, 비록 이러한 알고리즘은 다른 기본 분류기를 가지고 사용될 수 있다. 그러므로, 앞에 논문에서 boosting 또는 bagging으로 boosted 트리 또는 bagged 트리를 언급했다.
이 패키지는 전체 8개 함수로 구성된다, 각 메서드을 위한 3개 그리고 마진(margin) 그리고 evolerror. 각 메서드를 위한 3개의 함수: 부스팅 (또는 배깅) 분류기를 생성하고 그리고 훈련 집합에서 표본을 분리하기 위한 하나; 이전에 훈련된 앙상블을 사용하여 새로운 표본의 분류를 예측할 수 있는 하나; 그리고 마지막으로, 데이터 셋에서 이러한 분류기의 정밀도를 교차-검증으로 추정할 수 있는 다른 하나. 마지막으로, 각 관측에서 분류 예측에서 마진 그리고 오류 전개(error evolution)가 계산된다.
3.1. The boosting, predict.boosting and boosting.cv functions
전술 한 바와 같이, adabag 패키지에서 boosting 메서드에 대한 3개의 함수를 가지고 있다. 첫번째로 boosting 함수는 AdaBoost.M1 또는 SAMME를 사용하는 앙상블 분류기를 만들기 위해 그리고 훈련 표본에 분류를 지정하기 위해 이용할 수 있다. R에서 어떤 함수는 고정된 초기 인수의 집합이 요구된다; 이 경우에, 6개의 인수가 있다. formula, lm 함수에서 처럼, 종속 변수와 독립 변수를 판독한다. formula에서 명명된 변수를 해석하기 위한 데이터 프레임. 이것은 앙상블 훈련에서 사용할 데이터를 수집한다. 논리 인수 boos가 TRUE이면(기본으로), 훈련 집합의 부트스트랩 표본은 반복에서 각 관측을 위한 가중치를 사용하도록 한다. 만약 boos이 FALSE이면, 모든 관측에서 자신의 가중치를 가지고 사용된다. 정수 mfinal는 boosting을 실행하거나 사용할 트리의 수를 위한 반복 횟수를 설정한다 (기본으로 mfinal = 100 회 반복) .
만약 논리 인수 coeflearn = "Breiman" 이면 (기본), 그러면 alpha = 1 ⁄ 2 ln((1 − eb) ⁄ eb)을 사용한다. 어쨌든, coeflearn = "Freund" 이면, 그러면 alpha = ln((1 − eb) ⁄ eb)를 사용한다. 둘 모두에서 AdaBoost.M1 알고리즘은 적용되고 그리고 alpha는 계수(coefficient)를 갱신하는 가중치이다. 다른 한 편으로, 만약 coeflearn = "Zhu" 이면, SAMME 알고리즘은 alpha = ln((1 − eb) ⁄ eb) + ln(k − 1) 를 사용한다. 위에서 다루어진 것처럼, 단일 트리의 에러는 AdaBoost.M1에서는 범위 (0, 0.5) 안에 있다, SAMME는 범위 (0, 1 − 1 ⁄ k) 안에 있는 동안. 이러한 가정이 충족되지 않는 경우에, Opitz 와 Maclin (Opitz and Maclin 1999)는 모든 가중치가 같게 재설정 한다, 이러한 트리에서 가중치의 적당한 값을 선택하고 그리고 다시 진행한다. 같은 해결책이 여기에 적용되었다. eb = 0 일때, alpha 상수는 eb = 0.001 을 사용하여 계산 된다 그리고 eb ≥ 0.5 (SAMME 에서 eb ≥ 1 − 1 ⁄ k) 일 때, 0.499로 치환된다 (0.999 − 1 ⁄ k, 각각).
마지막으로, rpart 함수의 세부 사항을 조절하는 옵션 control 또한 앙상블에서 트리의 크기를 특별하게 제한하기 위하여 boosting에 전달된다. 더 상세한 내용은 rpart.control를 보라.
boosting 적용과 앙상블 훈련에, 이 함수는 클래스 객체 boosting을 출력한다, 7개의 컴포넌트를 가지는 목록. 첫번째 하나는 앙상블 훈련에 사용된 formula 이다, 두번째로, 반복으로 성장된 trees를 보여준다. 트리의 가중치를 서술하는 벡터. 선택 매트릭 설명, 각각의 관측에 대하여, 각 분류에 할당된 트리의 수, 각 분류에서 다달은 사후 확률(posterior probability)의 근사치. 이 확률 추정은 최종 앙상블에서 선택 또는 지지도의 비율을 사용하여 계산 된다. class 벡터는 앙상블 분류기에서 예측된 분류이다. 마지막으로 importance 벡터는 분류 작업에서 각 변수의 상관 중요도 또는 기어도를 반환한다.
boosting 함수는 예측자 변수의 상관 중요도를 정량화할 수 있도록 하는 점에 강조할 가치가 있다. 작은 개별 트리를 이해하는 것은 쉬울 수 있다. 어쨌든, boosting 앙상블에서 사용된 수백 또는 수천의 트리를 해석하는데 더 많은 어려움이 있다. 그리므로, 식별을 위해 예측 변수의 기여도를 정량화 할 수 있음은 실제로 중요한 이점이다. 중요도 측정은 트리에서 변수에 주어진 지니 지수(Gini index)의 이득과 그리고 boosting인 경우에 트리의 가중치로 한다. 이 목적을 위해, caret 패키지의 varImp 함수는 트리에서 변수의 지니 지수의 이득을 구하기 위해 사용된다.
잘 알려진 iris 데이터 셋은 adabag을 사용을 설명하는 예제로 이용 된다. 패키지는 library("adabag")를 사용하여 적재 되고 그리고 자동으로 프로그램은 요구되는 패키지 rpart, caret 그리고 mlbench (Leisch and Dimitriadou 2012) 를 호출한다.
데이터셋은 무작위로 두개의 같은 집합으로 나눠진다. 훈련 집합은 아래의 코드를 이용하여 최대 깊이 1 (stumps)의 10 개 트리의 boosting 앙상블을 가지고 분류 된다. 반환된 목록은 사용된 식으로 구성 된다, 10 개의 작은 트리 그리고 트리의 가중치. 트리의 가장 작은 에러, 가장 큰 그것의 가중치. 다른 말로, 트리의 가장 낮은 에러, 최종 앙상블에서 더 많은 관련. 이 경우에, 최고 가중치 (번호 3, 4, 5 그리고 6)를 가지는 440 개의 트리에 묶여 있다. 다른 한 편으로, 트리 번호 9는 가장 낮은 가중치 (0.175)을 가진다. 메트릭 votes 와 prob는 각 관측(행, row)이 각 분류(열, column)에 지정되는 가중된 선택과 확률을 보여 준다. 그러므로, 각 분류에서 확률은 68.62%, 31.38% 그리고 0% 이다, 각각, 그리고 할당된 분류는 class 벡터에서 볼 수 있는 것과 같은 "setosa" 이다.
R> library("adabag")
R> data("iris")
R> train <- c(sample(1:50, 25), sample(51:100, 25), sample(101:150, 25))
R> iris.adaboost <- boosting(Species ~ ., data = iris[train, ], mfinal = 10,
+ control = rpart.control(maxdepth = 1))
R> iris.adaboost
$formula
Species ~ .
$trees
$trees[[1]]
n = 75
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 75 46 virginica (0.29333333 0.32000000 0.38666667)
2) Petal.Length < 4.8 44 22 setosa (0.50000000 0.50000000 0.00000000) *
3) Petal.Length >= 4.8 31 2 virginica (0.00000000 0.06451613 0.93548387) *
$trees[[2]]
n= 75
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 75 40 versicolor (0.22666667 0.46666667 0.30666667)
2) Petal.Width < 1.7 53 18 versicolor (0.32075472 0.66037736 0.01886792) *
3) Petal.Width >= 1.7 22 0 virginica (0.00000000 0.00000000 1.00000000) *
...
$trees[[10]]
n= 75
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 75 42 virginica (0.21333333 0.34666667 0.44000000)
2) Petal.Width < 1.7 46 20 versicolor (0.34782609 0.56521739 0.08695652) *
3) Petal.Width >= 1.7 29 0 virginica (0.00000000 0.00000000 1.00000000) *
$weights
[1] 0.3168619 0.2589715 0.3465736 0.3465736 0.3465736 0.3465736 0.2306728
[8] 0.3168619 0.1751012 0.2589715
$votes
[,1] [,2] [,3]
[1,] 2.0200181 0.923717 0.0000000
[2,] 2.0200181 0.923717 0.0000000
...
[25,] 2.0200181 0.923717 0.0000000
[26,] 0.6337238 1.963438 0.3465736
[27,] 0.0000000 1.732765 1.2109701
...
[50,] 0.6337238 1.788337 0.5216748
[51,] 0.0000000 1.039721 1.9040144
[52,] 0.0000000 1.039721 1.9040144
...
[74,] 0.0000000 1.039721 1.9040144
[75,] 0.0000000 1.039721 1.9040144
$prob
[,1] [,2] [,3]
[1,] 0.6862092 0.3137908 0.0000000
[2,] 0.6862092 0.3137908 0.0000000
...
[25,] 0.6862092 0.3137908 0.0000000
[26,] 0.2152788 0.6669886 0.1177326
[27,] 0.0000000 0.588628 0.411372
...
[50,] 0.2152788 0.6075060 0.1772152
[51,] 0.0000000 0.3531978 0.6468022
[52,] 0.0000000 0.3531978 0.6468022
...
[74,] 0.0000000 0.3531978 0.6468022
[75,] 0.0000000 0.3531978 0.6468022
$class
[1] "setosa" "setosa" "setosa" "setosa" "setosa"
[6] "setosa" "setosa" "setosa" "setosa" "setosa"
[11] "setosa" "setosa" "setosa" "setosa" "setosa"
[16] "setosa" "setosa" "setosa" "setosa" "setosa"
[21] "setosa" "setosa" "setosa" "setosa" "setosa"
[26] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[31] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[36] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[41] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[46] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[51] "virginica" "virginica" "virginica" "virginica" "virginica"
[56] "virginica" "virginica" "virginica" "versicolor" "virginica"
[61] "virginica" "virginica" "virginica" "virginica" "virginica"
[66] "virginica" "virginica" "virginica" "versicolor" "versicolor"
[71] "virginica" "virginica" "versicolor" "virginica" "virginica"
$importance
Sepal.Length Sepal.Width Petal.Length Petal.Width
0 0 83.20452 16.79548
attr(,"class")
[1] "boosting"
importance 벡터에서 Petal.Length를 가장 중요한 변수로 찾을 수 있다, 정보 이득(information gain)에서 83.20% 이므로. 그것은 Figure 1에서 그래픽으로 보여 줄 수 있다.
R> barplot(iris.adaboost$imp[order(iris.adaboost$imp, decreasing = TRUE)], + ylim = c(0, 100), main = "Variables Relative Importance", + col = "lightblue")
 |
| Figure 1: iris 표본에서 boosting의 변수 연관 중요도 |
iris.adaboost 객체로 부터 훈련 집합의 혼동 행렬(confusion matrix)을 만들고 그리고 에러를 계산하기가 쉽다. 이 경우에, 분류 virginica로 부터 4개의 꽃이 versicolor로 구분된다, 그래서 도달한 에러는 5.33% 이다.
R> table(iris.adaboost$class, iris$Species[train],
+ dnn = c("Predicted Class", "Observed Class"))
Observed Class
Predicted Class setosa versicolor virginica
setosa 25 0 0
versicolor 0 25 4
virginica 0 0 21
R> 1 - sum(iris.adaboost$class == iris$Species[train]) /
+ length(iris$Species[train])
[1] 0.05333333
두번째 함수 predict.boosting는 제너릭 함수(generic function) predict의 변수를 연결한다 그리고 하더 더 (object,newdata,newmfinal = length(objects$trees),...)를 추가한다. 클래스 boosting의 적합된 모델 객체를 이용하여 데이터 프레임을 분류한다. 이것은 어떤 함수의 결과로 boosting 함수에서 반환된 같은 이름의 컴포넌트를 가지는 객체를 생성됨을 가정한다. newdata 인수는 예측에 필요한 값을 가지는 데이터 프레임이다. 식(formula(object))의 오른쪽에 언급된 예측자는 같은 이름을 가지고 여기에서 표현된다. 이 방법은, 훈련 데이터를 제외한 예측을 만들 수 있다. newmfinal 옵션은 예측에서 사용되는 boosting 객체의 트리 수를 고정한다. 이것은 사용자가 앙상블에 가지치기를 허락한다. 기본적으로, 객체에 모든 트리가 사용된다. 마지막으로, 3개의 점은 더 많은 인수가 다른 메서드로 전달되거나 전달 받는 일을 처리한다.
다른 한 편으로, 이 함수는 predict.boosting 클래스의 객체를 반환한다, 다음의 6개의 컴포넌트를 가지는 목록. 그들중 4개: formula, votes, prob 그리고 class는 boosting 출력에서와 같은 의미를 가진다. 게다가, confusion 행렬은 예측된 하나를 가지고 실제 분류를 비교한다 그리고, 마지막으로, 평균 error가 계산된다.
예제를 따라, iris.adaboost 분류기는 predict.boosting 함수를 수단으로 새로운 iris 표본을 위한 분류를 예측하는데 사용 할 수 있다, 아래에 보여주는 것처럼 그리고 앙상블은 가지칠 수 있다. 출력의 처음 4개의 컴포넌트는 이전 함수의 결과와 공통이다 그러나 혼동 행렬(confusion matrix) 그리고 검증 데이터 셋 에러는 여기서 추가적으로 제공된다. 이 경우에, 검증 데이터 집합에서 3개의 virginica iris는 versicolor로 분류되었다, 그래서 에러는 이 경우에 4%에 달한다.
R> iris.predboosting <- predict.boosting(iris.adaboost,
+ newdata = iris[-train, ])
R> iris.predboosting
$formula
Species ~ .
$votes
[,1] [,2] [,3]
[1,] 2.0200181 0.923717 0.0000000
[2,] 2.0200181 0.923717 0.0000000
...
[25,] 2.0200181 0.923717 0.0000000
[26,] 0.6337238 1.963438 0.3465736
[27,] 0.6337238 1.963438 0.3465736
...
[50,] 0.6337238 1.963438 0.3465736
[51,] 0.0000000 1.039721 1.9040144
[52,] 0.0000000 1.039721 1.9040144
...
[74,] 0.0000000 1.039721 1.9040144
[75,] 0.0000000 1.039721 1.9040144
$prob
[,1] [,2] [,3]
[1,] 0.6862092 0.3137908 0.0000000
[2,] 0.6862092 0.3137908 0.0000000
...
[25,] 0.6862092 0.3137908 0.0000000
[26,] 0.2152788 0.6669886 0.1177326
[27,] 0.2152788 0.6669886 0.1177326
...
[50,] 0.2152788 0.6669886 0.1177326
[51,] 0.0000000 0.3531978 0.6468022
[52,] 0.0000000 0.3531978 0.6468022
...
[74,] 0.0000000 0.3531978 0.6468022
[75,] 0.0000000 0.3531978 0.6468022
$class
[1] "setosa" "setosa" "setosa" "setosa" "setosa"
[6] "setosa" "setosa" "setosa" "setosa" "setosa"
[11] "setosa" "setosa" "setosa" "setosa" "setosa"
[16] "setosa" "setosa" "setosa" "setosa" "setosa"
[21] "setosa" "setosa" "setosa" "setosa" "setosa"
[26] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[31] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[36] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[41] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[46] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[51] "virginica" "virginica" "virginica" "virginica" "versicolor"
[56] "virginica" "virginica" "virginica" "virginica" "virginica"
[61] "virginica" "virginica" "virginica" "virginica" "versicolor"
[66] "virginica" "virginica" "virginica" "versicolor" "virginica"
[71] "virginica" "virginica" "virginica" "virginica" "virginica"
$confusion
Observed Class
Predicted Class setosa versicolor virginica
setosa 25 0 0
versicolor 0 25 3
virginica 0 0 22
$error
[1] 0.04
마지막으로, 세번째 함수 boosting.cv는 boosting을 가지는 v-fold 교차 검증(cross validation)을 실행한다. 교차 검증에서 일반적으로, 데이터는 거의 동일한 크기의 ν개의 겹치지 않는 하위집합(ν non-overlapping subsets)으로 나눠진다. 그러면 boosting에 하위집합 (ν − 1)으로 적용된다. 마지막으로, 예측은 왼쪽 부분 바깥의 하위집합으로 만들어진다. 그리고 ν 하위집합의 각각 하나에서 반복하며 진행된다.
이 함수의 인수는 boosting과 같은 7개 이다 그리고 하나 더, 정수 ν, ν-fold 교차 검증의 타입을 명확히 한다. 기본값은 0 이다. 이와 반대로, 만약 v를 관측 수와 같게 놓으면, leave-one-out 교차 검증이 수행된다. 이 외에도, 2와 관측의 개수 사이의 모든 값은 유효하다 그리고 모든 ν 관측의 제외하는 하나는 왼쪽에서 제외된다. boosting.cv 클래스의 객체가 제공된다, 3개 컴포넌트, class, confusion 그리고 error를 가지는 목록, predict.boosting 함수에서 이전에 설명을 가짐.
그러므로, 교차 검증은 이용 가능한 데이터 셋을 훈련과 검증의 하위집합으로 나눔 없이 앙상블 에러를 추정하기 위해 사용할 수 있다. 이것은 작은 데이터 셋에서 특히 유리하다.
iris 예의 실행에서, 10-folds 교차 검증이 트리의 수와 크기를 다루려고 적용되었다. 출력 컴포넌트는: 할당된 class(분류)를 가지는 벡터, 혼동 행렬(confusion matrix) 그리고 에러 평균(error mean). 이 경우에, versicolor로 분류된 4개의 virginica 꽃이 있다 그리고 3개의 versicolor는 virginica로 분류되었다, 그래서 추정된 에러는 4.67%에 달한다.
R> iris.boostcv <- boosting.cv(Species ~ ., v = 10, data = iris, mfinal = 10,
+ control = rpart.control(maxdepth = 1))
R> iris.boostcv
$class
[1] "setosa" "setosa" "setosa" "setosa" "setosa"
[6] "setosa" "setosa" "setosa" "setosa" "setosa"
...
[71] "virginica" "versicolor" "versicolor" "versicolor" "versicolor"
[76] "versicolor" "versicolor" "virginica" "versicolor" "versicolor"
[81] "versicolor" "versicolor" "versicolor" "virginica" "versicolor"
...
[136] "virginica" "virginica" "virginica" "versicolor" "virginica"
[141] "virginica" "virginica" "virginica" "virginica" "virginica"
[146] "virginica" "virginica" "virginica" "virginica" "virginica"
$confusion
Observed Class
Predicted Class setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 4
virginica 0 3 46
$error
[1] 0.04666667
3.2. The bagging, predict.bagging and bagging.cv functions
boosting과 같은 방법으로, bagging는 adabag에서 3개의 함수를 가진다. bagging 함수는 앙상블 분류기의 이런 종류를 생성하고 훈련 표본에 분류를 할당한다. 4개의 초기 변수는 (formula, data, mfinal 그리고 control) boosting 함수에서 처럼 같은 의미를 가진다. boosting과 닮지 않은 콕 집고 넘어가야 할 점은, 개별 분류기는 bagging에서 그들 사이에 독립이다는 것이다.
이 함수는 클래스 bagging의 객체를 만든다, boosting 처럼 대부분 같은 컴포넌트를 가지는 목록이다. 오로지 다른 것은 트리의 가중치 대신에 반복을 따라 사용되는 bootstrap 표본을 가지는 행렬이다.
iris 예제를 따라, bagging 분류기는 훈련 집합을 위한 다음 코드를 사용하는 최대 깊이 1(stumps)의 10개 트리를 가지게 생성 된다. 이 함수는 사용된 formula, 10개의 stumps 그리고 매트릭스 votes 와 prob를 가지는 목록을 반환한다. 이런 행렬은 각 관측 (행, row)이 각 분류 (열, column)으로 받은 선택 (확률) (votes probabilities)을 보여준다. 예로, 관측 26은 첫번째, 두번째 그리고 세번째 분류에서 각각 1, 5, 그리고 4를 선택 받았다. 그러므로, 그것의 확률은 0.1, 0.5 그리고 0.4 이다, 각각, 그리고, 따라서, 할당된 분류는 class 벡터에서 보여주는 것 처럼 versicolor 이다. 행렬 samples는 앙상블을 위해 사용된 10회 bootstrap 복제에서 선택된 관측을 보여준다.
R> iris.bagging <- bagging(Species ~ ., data = iris[train, ], mfinal = 10,
+ control = rpart.control(maxdepth = 1))
R> iris.bagging
$formula
Species ~ .
$trees
$trees[[1]]
n= 75
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 75 47 setosa (0.3733333 0.3333333 0.2933333)
2) Petal.Length< 2.45 28 0 setosa (1.0000000 0.0000000 0.0000000) *
3) Petal.Length>=2.45 47 22 versicolor (0.0000000 0.5319149 0.4680851) *
$trees[[2]]
n= 75
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 75 46 setosa (0.3866667 0.2933333 0.3200000)
2) Petal.Length< 2.35 29 0 setosa (1.0000000 0.0000000 0.0000000) *
3) Petal.Length>=2.35 46 22 virginica (0.0000000 0.4782609 0.5217391) *
...
$trees[[10]]
n= 75
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 75 45 versicolor (0.3066667 0.4000000 0.2933333)
2) Petal.Length< 2.45 23 0 setosa (1.0000000 0.0000000 0.0000000) *
3) Petal.Length>=2.45 52 22 versicolor (0.0000000 0.5769231 0.4230769) *
$votes
[,1] [,2] [,3]
[1,] 9 1 0
[2,] 9 1 0
...
[25,] 9 1 0
[26,] 1 5 4
[27,] 1 5 4
...
[50,] 1 5 4
[51,] 0 4 6
[52,] 0 4 6
...
[74,] 0 4 6
[75,] 0 4 6
$prob
[,1] [,2] [,3]
[1,] 0.9 0.1 0
[2,] 0.9 0.1 0
...
[25,] 0.9 0.1 0
[26,] 0.1 0.5 0.4
[27,] 0.1 0.5 0.4
...
[50,] 0.1 0.5 0.4
[51,] 0 0.4 0.6
[52,] 0 0.4 0.6
...
[74,] 0 0.4 0.6
[75,] 0 0.4 0.6
$class
[1] "setosa" "setosa" "setosa" "setosa" "setosa"
[6] "setosa" "setosa" "setosa" "setosa" "setosa"
[11] "setosa" "setosa" "setosa" "setosa" "setosa"
[16] "setosa" "setosa" "setosa" "setosa" "setosa"
[21] "setosa" "setosa" "setosa" "setosa" "setosa"
[26] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[31] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[36] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[41] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[46] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[51] "virginica" "virginica" "virginica" "virginica" "virginica"
[56] "versicolor" "virginica" "versicolor" "virginica" "virginica"
[61] "virginica" "virginica" "virginica" "virginica" "virginica"
[66] "virginica" "virginica" "virginica" "virginica" "virginica"
[71] "virginica" "virginica" "virginica" "virginica" "virginica"
$samples
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 8 21 53 16 75 71 15 47 73 7
[2,] 58 60 65 36 51 18 29 74 65 4
[3,] 74 21 22 24 72 14 34 27 22 26
[4,] 39 26 6 16 66 29 70 32 1 28
[5,] 26 17 42 36 53 4 46 75 21 22
...
[71,] 3 28 13 55 53 23 64 17 27 36
[72,] 23 24 53 54 42 53 2 44 48 32
[73,] 16 17 69 12 50 15 34 30 7 42
[74,] 43 46 29 70 50 37 61 50 73 35
[75,] 45 44 13 75 19 67 49 68 1 67
$importance
Sepal.Length Sepal.Width Petal.Length Petal.Width
0 0 79.69223 20.30777
attr(,"class")
[1] "bagging"
boosting을 가지는 라인에서, 가장 큰 기여를 하는 변수는 Petal.Length (79.69%) 그리고 Petal.Width (20.31%) 이다. 반대로, 다른 2개의 변수의 기여는 0 이다. 그것은 Figure 2에서 그림으로 보여준다.
R> barplot(iris.bagging$imp[order(iris.bagging$imp, decreasing = TRUE)], + ylim = c(0, 100), main = "Variables Relative Importance", + col = "lightblue")
 |
| Figure 2: iris 예에서 bagging의 변수 연관 중요도 |
객체 iris.bagging은 혼동 행렬(confusion matrix)과 훈련 집합 에러를 계산하기 위해 사용된다. 알 수 있는 바와 같이, 단지 2개의 경우가 잘못 분류 되었다 (2개의 virginica 꽂이 versicolor로 분류 되었다), 그리므로 에러는 2.67% 이다.
R> table(iris.bagging$class, iris$Species[train],
+ dnn = c("Predicted Class", "Observed Class"))
Observed Class
Predicted Class setosa versicolor virginica
setosa 25 0 0
versicolor 0 25 2
virginica 0 0 23
R> 1 - sum(iris.bagging$class == iris$Species[train]) /
+ length(iris$Species[train])
[1] 0.02666667
게다다, predict.bagging은 predict.boosting 처럼 같은 인수와 값을 가진다. 어쨌든, 그것은 적합된 bagging 객체를 호출하고 그리고 클래스 predict.bagging의 객체를 반환한다. 마지막으로, bagging.cv는 bagging을 가지고 ν-fold 교차 검증(&nu-fold cross validation)을 실행한다. 다시, ν-fold 교차 검증의 타입은 bagging 함수의 인수로 추가된다. 게다가, 출력은 boosting.cv과 비슷한 클래스 bagging.cv의 객체이다.
함수 predict.bagging는 훈련 집합에서 각 관측의 분류를 예측하고 그리고 그것을 가지치기 위해 미리 생성된 객체 iris.bagging을 이용한다, 만약 필요하면. 출력은 predict.boosting에서와 같다. 이 경우에, confusion 행렬은 versicolor로 분류된 2개의 virginica 그리고 반대로 보여준다. 그래서 error는 5.33% 이다.
R> iris.predbagging <- predict.bagging(iris.bagging, newdata = iris[-train, ])
R> iris.predbagging
$formula
Species ~ .
$votes
[,1] [,2] [,3]
[1,] 9 1 0
[2,] 9 1 0
...
[26,] 1 5 4
[27,] 1 5 4
...
[74,] 0 4 6
[75,] 0 4 6
$prob
[,1] [,2] [,3]
[1,] 0.9 0.1 0
[2,] 0.9 0.1 0
...
[26,] 0.1 0.5 0.4
[27,] 0.1 0.5 0.4
...
[74,] 0 0.4 0.6
[75,] 0 0.4 0.6
$class
[1] "setosa" "setosa" "setosa" "setosa" "setosa"
[6] "setosa" "setosa" "setosa" "setosa" "setosa"
[11] "setosa" "setosa" "setosa" "setosa" "setosa"
[16] "setosa" "setosa" "setosa" "setosa" "setosa"
[21] "setosa" "setosa" "setosa" "setosa" "setosa"
[26] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[31] "versicolor" "versicolor" "versicolor" "versicolor" "virginica"
[36] "versicolor" "virginica" "versicolor" "versicolor" "versicolor"
[41] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[46] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[51] "virginica" "virginica" "virginica" "virginica" "virginica"
[56] "virginica" "virginica" "virginica" "virginica" "virginica"
[61] "virginica" "versicolor" "virginica" "virginica" "versicolor"
[66] "virginica" "virginica" "virginica" "virginica" "virginica"
[71] "virginica" "virginica" "virginica" "virginica" "virginica"
$confusion
Observed Class
Predicted Class setosa versicolor virginica
setosa 25 0 0
versicolor 0 23 2
virginica 0 2 23
$error
[1] 0.05333333
다음은, 10-folds 교차 검증이 bagging에서 적용 되었다, 트리의 수와 크기를 유지함. 이 경우에, versicolor로 분류된 12개의 virginica 종이 있다 그리고 virginica로 분류된 7개의 versicolor 등, 추정된 error는 12.66%에 달한다.
R> iris.baggingcv <- bagging.cv(Species ~ ., v = 10, data = iris,
+ mfinal = 10, control = rpart.control(maxdepth = 1))
R> iris.baggingcv
$class
[1] "setosa" "setosa" "setosa" "setosa" "setosa"
...
[56] "virginica" "versicolor" "versicolor" "versicolor" "versicolor"
[61] "versicolor" "versicolor" "versicolor" "versicolor" "versicolor"
[66] "virginica" "versicolor" "versicolor" "versicolor" "versicolor"
...
[136] "virginica" "virginica" "virginica" "versicolor" "virginica"
[141] "virginica" "virginica" "versicolor" "virginica" "virginica"
[146] "virginica" "virginica" "virginica" "virginica" "virginica"
$confusion
Clase real
Clase estimada setosa versicolor virginica
setosa 50 0 0
versicolor 0 43 12
virginica 0 7 38
$error
[1] 0.1266667
3.3. The margins and errorevol functions
앞에서 말한 중요성 때문에 margins 함수는 이전에 정의한 방정식 4에서 처럼 데이터 프레임에 boosting 또는 bagging의 마진을 계산하기 위해 adabag에 추가되었다.
- object. 이 객체는 함수 bagging, boosting, predict.bagging 또는 predict.boosting 중 하나의 결과 이여야 한다. 이것은 formula 그리고 class으로 명명되는 적어도 2개의 컴포넌트를 가지는 객체를 생성하는 어떤 함수의 결과로 가정한다, bagging 함수의 인스턴스에서 반환된 것과 같음.
- newdata. 객체를 생성하기 위해 사용된 같은 데이터 프레임.
출력은, 클래스 margins의 객체, margin이 있는 단지 하나의 벡터를 가지는 단순한 목록이다. 아래에 이전 절에서 만든 bagging 분류기의 마진을 계산하는 코드를 보여준다, 훈련과 검증 집합에서, 각각. 음의 마진을 가지는 예는 잘못 분류되어 있는 것들이다. 그것은 이전에 말한 바와 같이, 각 집합에 2개 또는 4개의 경우가 있다, 각각.
R> iris.bagging.margins <- margins(iris.bagging, iris[train, ]) R> iris.bagging.predmargins <- margins(iris.predbagging, iris[-train, ]) R> iris.bagging.margins $margins [1] 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 [15] 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.1 0.1 0.1 [29] 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 [43] 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.2 0.2 0.2 0.2 0.2 -0.1 [57] 0.2 -0.1 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 [71] 0.2 0.2 0.2 0.2 0.2 R> iris.bagging.predmargins $margins [1] 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 [15] 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.1 0.1 0.1 [29] 0.1 0.1 0.1 0.1 0.1 0.1 -0.2 0.1 -0.2 0.1 0.1 0.1 0.1 0.1 [43] 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.2 0.2 0.2 0.2 0.2 0.2 [57] 0.2 0.2 0.2 0.2 0.2 -0.1 0.2 0.2 -0.1 0.2 0.2 0.2 0.2 0.2 [71] 0.2 0.2 0.2 0.2 0.2
Figure 3은 이 응용(application)에서 개발된 bagging 분류기에서 마진의 누적 분포를 보여준다, 파란색 선은 훈련 집합에 그리고 초록색 선은 검증 집합에 해당하는 경우. bagging에서, 파란색 음의 마진의 2.66%가 훈련 에러와 일치하고 그리고 초록색 음수의 5.33%가 검증 에러와 하나이다.
R> margins.test <- iris.bagging.predmargins[[1]]
R> margins.train <- iris.bagging.margins[[1]]
R> plot(sort(margins.train),
+ (1:length(margins.train)) / length(margins.train),
+ type = "l", xlim = c(-1,1),
+ main = "Margin cumulative distribution graph", xlab = "m",
+ ylab = "% observations", col = "blue3", lwd = 2)
R> abline(v = 0, col = "red", lty = 2, lwd = 2)
R> lines(sort(margins.test), (1:length(margins.test)) / length(margins.test),
+ type = "l", cex = 0.5, col = "green", lwd = 2)
R> legend("topleft", c("test","train"), col = c("green", "blue"), lty = 1,
+ lwd = 2)
 |
| Figure 3: iris 예에서 bagging의 마진 |
패키지의 현재 버전에서, 마지막 함수는 앙상블 크기가 성장함에 따라 데이터 프레임에 AdaBoost.M1, AdaBoost-SAMME 또는 bagging 분류기의 에러 전개(error evolution)를 계산하는 errorevol 이다. 이 함수는 margins과 같은 2개의 인수를 가진다 그리고 에러 전개가 있는 단지 하나의 벡터를 가지는 목록을 출력한다. 이 정보는 bagging 그리고 boosting이 앙상블 에러가 얼마나 빨리 감소하는지 보기 위해 유용할 수 있다. 게다가, 그것은 과적합의 존재를 찾을 수 있고 그리고, 이 경우에, 연관되는 predict 함수를 사용하는 앙상블의 가지치기의 편리함. 비록 앙상블의 작은 크기로 인해, 이 예제는 에러 전개(error evolution)의 유용함을 보여주는 가장 적당한 경우가 아니다, 그것은 단지 보여주는 목적으로 사용되었다.
R> evol.test <- errorevol(iris.adaboost, iris[-train, ])
R> evol.train <- errorevol(iris.adaboost, iris[train, ])
R> plot(evol.test$error, type = "l", ylim = c(0, 1),
+ main = "Boosting error versus number of trees", xlab = "Iterations",
+ ylab = "Error", col = "red", lwd = 2)
R> lines(evol.train$error, cex = .5, col = "blue", lty = 2, lwd = 2)
R> legend("topleft", c("test", "train"), col = c("red", "blue"), lty = 1:2,
+ lwd = 2)
 |
| Figure 4: iris 예제에서 boosting의 에러 전개 |
4. Examples
패키지 adabag을 다른 분류 예제를 통해서 지금 깊게 설명한다. 첫번째 예는 Hastie, Tibshirani, 그리고 Friedman (2001, pp. 301-309) 그리고 Culp, Johnson, 그리고 Michailides (2006)에서 사용된 이전 시뮬레이트한 데이터셋을 사용하는 이분법적 분류 문제(dichotomous classification problem)를 보여준다. 두번째 예는 기계 학습 데이터베이스의 UCI 저장소에 있는 4개의 분류 데이터이다. 이 예제와 iris는 base 와 mlbench R 패키지에서 이용 가능하다.
4.1. 이분법 예제 (A dichotomous example)
2개의 분류로 시뮬레이트된 데이터 셋은 다음과 같이 정의된 특징 그리고 2개의 분류로 사용되는 10개의 표준 독립 가우시안으로 구성된다:
여기에 값 9.34는 자유도 10을 가지는 카이-제곱 랜덤 변수의 중앙값이다 (10개의 표준 가우시안의 제곱합). 2,000개의 훈련 그리고 10,000개의 검증 건이 있다, 거의 균등한. 더 잘 비교하기 위해, stumps는 약한 분류기와 400회 반복으로 Hastie et al. (2001) 그리고 Culp et al. (2006)와 같게 실행된다. coeflearn("Breiman", "Freund" or "Zhu") 그리고 boos (TRUE or FALSE)가 있다. k = 2 분류이므로 Freund와 Zhu 옵션은 완전히 동등하다, 나중에 이 예에서 고려되 않는다. 변수의 4개의 가능한 조합의 코드는 첨부 파일에서 이용 가능하고, 그리고 주요 결과의 요약은 아래에 보여준다.
R> n <- 12000
R> p <- 10
R> set.seed(100)
R> x <- matrix(rnorm(n * p), ncol = p)
R> y <- as.factor(c(-1, 1)[as.numeric(apply(x^2, 1, sum) > 9.34) + 1])
R> data <- data.frame(y, x)
R> train <- sample(1:n, 2000, FALSE)
R> formula <- y ~ .
R> vardep <- data[ , as.character(formula[[2]])]
R> cntrl <- rpart.control(maxdepth = 1, minsplit = 0, cp = -1)
R> mfinal <- 400
R> data.boosting <- boosting(formula = formula, data = data[train, ],
+ mfinal = mfinal, coeflearn = "Breiman", boos = TRUE,
+ control = cntrl)
R> data.boostingBreimanTrue <- data.boosting
R> table(data.boosting$class, vardep[train],
+ dnn = c("Predicted Class", "Observed Class"))
Observed Class
Predicted Class -1 1
-1 935 281
1 55 729
R> 1 - sum(data.boosting$class == vardep[train]) / length(vardep[train])
[1] 0.168
R> data.predboost <- predict.boosting(data.boosting, newdata = data[-train, ])
R> data.predboost$confusion
Observed Class
Predicted Class -1 1
-1 4567 1468
1 460 3505
R> data.predboost$error
[1] 0.1928
R> data.boosting$imp
X1 X2 X3 X4 X5 X6 X7
10.541101 11.211198 11.195706 14.000324 8.161411 15.087848 4.827447
X8 X9 X10
8.506216 7.433147 9.035603
R> data.boosting <- boosting(formula = formula, data = data[train, ],
+ mfinal = mfinal, coeflearn = "Freund", boos = FALSE,
+ control = cntrl)
R> data.boostingFreundFalse <- data.boosting
R> table(data.boosting$class, vardep[train], dnn = c("Predicted Class",
+ "Observed Class"))
Observed Class
Predicted Class -1 1
-1 952 78
1 38 932
R> 1 - sum(data.boosting$class == vardep[train]) / length(vardep[train])
[1] 0.058
R> data.predboost <- predict.boosting(data.boosting, newdata = data[-train,])
R> data.predboost$confusion
Observed Class
Predicted Class -1 1
-1 4498 613
1 529 4360
R> data.predboost$error
[1] 0.1142
R> data.boosting$imp
X1 X2 X3 X4 X5 X6 X7
10.071340 9.884980 10.874889 10.625273 11.287803 10.208411 8.716455
X8 X9 X10
8.093104 9.706120 10.531625
| Options | 400 Iterations | Mininum (Iterations) |
| "Breiman"/FALSE | 15.36 | 15.15 (374) |
| "Breiman"/TRUE | 19.28 | 17.20 (253) |
| "Freund"/FALSE | 11.42 | 11.42 (398) |
| "Freund"/TRUE | 16.84 | 16.05 (325) |
| Table 4: 검증 에러 백분율. | ||
400회째 반복(Table 4)에 조합으로 다루이진 4개의 검증 에러는 15.36%, 19.28%, 11.42% 그리고 16.84% 이다, 각각. 그러므로 정확성의 조건에서 승리 조합은 coeflearn = "Freund" 그리고 boos = FALSE를 가지는 boosting 이다. 이런 변수의 쌍의 결과는 Hastie et al. (2001) 과 Culp et al.(2006)에서 얻어진 것과 비슷하다, 12.2% 그리고 11.1%, 각각. 게다다, 훈련 에러(5.8%)는 Culp et al의 달성한 값에 근접한다, (6%).
게다가, Table 4는 진행에서 최소 에러와 그리고 이 최소값에 도달하는 반복 수를 보여준다. 이것은 errorevol 함수 덕분에 가능하다. Freund-FALSE의 (Figure 7) 짝이 가장 낮은 검증 에러를 달성하고 그리고 이 값이 훈련 과정의 거의 끝에서 일치한다는 것에 주목할 가치가 있다. 그러므로, 최적의 값에 아직 도착하지 못해다는 근거있는 생각이 될 수 있다. 4개의 조합에서 에러의 전개는 Figures 5, 6, 7 그리고 8에서 그림으로 보여준다, 각각의 경우 아래의 코드를 실행하여 생성된다.
R> data.boosting <- data.boostingFreundFalse
R> errorevol.train <- errorevol(data.boosting, data[train, ])
R> errorevol.test <- errorevol(data.boosting, data[-train, ])
R> plot(errorevol.test[[1]], type = "l", ylim = c(0, 0.5),
+ main = "Adaboost error versus number of trees", xlab = "Iterations",
+ ylab = "Error", col = "red", lwd = 2)
R> lines(errorevol.train[[1]], cex = 0.5, col = "blue", lty = 1, lwd = 2)
R> legend("topright", c("test", "train"), col = c("red", "blue"), lty = 1,
+ lwd = 2)
R> abline(h = min(errorevol.test[[1]]), col = "red", lty = 2, lwd = 2)
R> abline(h = min(errorevol.train[[1]]), col = "blue", lty = 2, lwd = 2)
 |
| Figure 5: AdaBoost 에러 대 "Breiman"/FALSE 옵션의 트리 수. |
 |
| Figure 6: AdaBoost 에러 대 "Breiman"/TRUE 옵션의 트리 수. |
 |
| Figure 7: AdaBoost 에러 대 "Freund"/FALSE 옵션의 트리 수. |
 |
| Figure 8: AdaBoost 에러 대 "Freund"/TRUE 옵션의 트리 수. |
옵션 Breiman/TRUE (Figure 6)에서 400회 반복 훨씬 전에 최적의 결과에 도달했다 그리고 과적합의 분명한 예제를 명확히 보여주는 253 반복 이후에 증가가 시작한다.
R> data.prune <- predict.boosting(data.boosting, newdata = data[-train, ],
+ newmfinal = 253)
R> data.prune$confusion
Observed Class
Predicted Class -1 1
-1 4347 1040
1 680 3933
R> data.prune$error
[1] 0.172
4.2. 다중분류 예 (A multiclass example)
이분법의 경우를 넘어서는 문제를 푸는데 이 패키지의 유용성을 보여주기 위해, 4개의 분류 예를 이 절에서 사용한다. 이 문제는 iris의 경우 보더 더 상당히 더 복잡한 문제에서 함수 사용을 설명하여 도움을 줄 것이다. 특히, UCI 저장소에서 다운 받은 Vehicle 데이터 셋이 적용되었다. 이 데이터 셋은 864개 표본을 가지고 있고 그리고 목적은 4개의 타입(bus, opel, saab 그리고 van) 중 하나로 주어진 자동차 실루엣에서 분류해야 한다, 실루엣에서 뽑은 18개의 숫치 특징의 집합을 사용.
앙상블 사용의 이점을 보여줄 목적에서, 단일 트리의 결과를 boosting 과 bagging을 가지고 얻은 것과 비교한다. 단일 트리는 rpart 패키지의 방법으로 만들었다, adabag 패키지를 적재할 때 자동으로 호출됨. 많은 수의 분류 때문에, 최대 깊이 5를 가지는 트리가 단일과 앙상블 건 둘 모두에 사용된다. 앙상블은 50개의 트리를 구성한다.
4개 메서드의 에러를 비교하기 위해, 50회 반복이 실행되고 그리고 평균 결과가 계산된다. 다른 한 편으로, 앙상블의 어떤 특징을 분석하기 위해, 변수 연관 중요도 그리고 마진 같은, 특정 모델이 필요하다, 그래서 최소 에러에 도달한 모델이 사용된다.
Table 5에서 단일 트리는, 평균 검증 에러 32.39%를 가짐, 배깅에 패배했다, 27.4% 그리고 매우 낮은 에러를 가지는 Adaboost.M1 와 SAMME 각각에 뒤쳐지는 것으로 결론 났다, 23.94% 그리고 24.25%, 각각. 마지막으로, 각 메서드로 도달한 최소 에러를 주목, 가장 낮은 검증 에러는 다중분류 경우에 적응을 보장함을 보여주는 SAMME 알고리즘의 17.73% 이다. 어쨌든, 2개의 boosting 메서드 사이에 큰 차이는 없다.
| CART | Bagging | AdaBoost.M1 | SAMME | |
| mean | 0.3239007 | 0.2740426 | 0.2394326 | 0.2425532 |
| s.d. | 0.0299752 | 0.0274216 | 0.0225558 | 0.0292594 |
| min. | 0.2553191 | 0.2021277 | 0.1914894 | 0.1773050 |
| max. | 0.3971631 | 0.3262411 | 0.2872340 | 0.2943262 |
| Table 5: 50회 반복에서 검증 에러. | ||||
R> data("Vehicle")
R> l <- length(Vehicle[ , 1])
R> sub <- sample(1:l, 2 * l/3)
R> maxdepth <- 5
R> Vehicle.rpart <- rpart(Class~., data = Vehicle[sub,], maxdepth = maxdepth)
R> Vehicle.rpart.pred <- predict(Vehicle.rpart, newdata = Vehicle,
+ type = "class")
R> 1 - sum(Vehicle.rpart.pred[sub] == Vehicle$Class[sub]) /
+ length(Vehicle$Class[sub])
[1] 0.2464539
R> tb <- table(Vehicle.rpart.pred[-sub], Vehicle$Class[-sub])
R> tb
bus opel saab van
bus 62 3 3 0
opel 3 26 6 1
saab 3 29 50 5
van 5 5 9 72
R> 1 - sum(Vehicle.rpart.pred[-sub] == Vehicle$Class[-sub]) /
+ length(Vehicle$Class[-sub])
[1] 0.2553191
R> mfinal <- 50
R> cntrl <- rpart.control(maxdepth = 5, minsplit = 0, cp = -1)
R> Vehicle.bagging <- bagging(Class ~ ., data = Vehicle[sub, ],
+ mfinal = mfinal, control = cntrl)
R> 1 - sum(Vehicle.bagging$class == Vehicle$Class[sub]) /
+ length(Vehicle$Class[sub])
[1] 0.1365248
R> Vehicle.predbagging <- predict.bagging(Vehicle.bagging,
+ newdata = Vehicle[-sub, ])
R> Vehicle.predbagging$confusion
Observed Class
Predicted Class bus opel saab van
bus 68 3 3 0
opel 1 33 9 1
saab 0 31 48 2
van 0 3 4 76
R> Vehicle.predbagging$error
[1] 0.2021277
R> Vehicle.adaboost <- boosting(Class ~., data = Vehicle[sub, ],
+ mfinal = mfinal, coeflearn = "Freund", boos = TRUE,
+ control = cntrl)
R> 1 - sum(Vehicle.adaboost$class == Vehicle$Class[sub])/
+ length(Vehicle$Class[sub])
[1] 0
R> Vehicle.adaboost.pred <- predict.boosting(Vehicle.adaboost,
+ newdata = Vehicle[-sub,])
R> Vehicle.adaboost.pred$confusion
Observed Class
Predicted Class bus opel saab van
bus 68 1 0 0
opel 1 41 22 3
saab 0 21 49 0
van 1 3 2 70
R> Vehicle.adaboost.pred$error
[1] 0.1914894
R> Vehicle.SAMME <- boosting(Class ~ ., data = Vehicle[sub, ],
+ mfinal = mfinal, coeflearn = "Zhu", boos = TRUE,
+ control = cntrl)
R> 1 - sum(Vehicle.SAMME$class == Vehicle$Class[sub]) /
+ length(Vehicle$Class[sub])
[1] 0
R> Vehicle.SAMME.pred <- predict.boosting(Vehicle.SAMME,
+ newdata = Vehicle[-sub, ])
R> Vehicle.SAMME.pred$confusion
Observed Class
Predicted Class bus opel saab van
bus 71 0 0 0
opel 1 43 24 1
saab 0 21 46 0
van 0 2 1 72
R> Vehicle.SAMME.pred$error
[1] 0.177305
bagging과 다른 두 분류기에서 연관 중요도 측정의 비교, 2개의 최소 중요도 변수를 강조함에 일치한다. Max.L.Ra는 bagging 그리고 AdaBoost.M1 그리고 SAMME의 두번째 하나에서 가강 큰 기여를 한다. Figures 9, 10 그리고 11은 그것의 상관 중요도 값으로 순위를 매긴 변수를 보여준다.
R> sort(Vehicle.bagging$importance, decreasing = TRUE)
Max.L.Ra Sc.Var.maxis Elong Comp Max.L.Rect Sc.Var.Maxis
20.06153052 11.34898853 9.85195343 8.21094638 7.90785330 5.71291406
D.Circ Scat.Ra Circ Pr.Axis.Ra Skew.maxis Skew.Maxis
5.47042335 5.23492044 4.62644012 4.32449318 3.84967772 3.46614732
Kurt.maxis Kurt.Maxis Ra.Gyr Rad.Ra Holl.Ra Pr.Axis.Rect
2.98563804 2.09313159 1.70889907 1.56229729 1.54524768 0.03849798
R> sort(Vehicle.adaboost$importance,decreasing = TRUE)
Max.L.Ra Elong Max.L.Rect Pr.Axis.Ra Sc.Var.maxis Scat.Ra
12.0048265 8.2118048 8.1391111 7.2979696 6.8809291 6.8360291
D.Circ Sc.Var.Maxis Comp Skew.maxis Rad.Ra Ra.Gyr
6.6569366 6.3137727 6.2558542 4.9731790 4.6792429 4.5205229
Kurt.maxis Skew.Maxis Circ Kurt.Maxis Holl.Ra Pr.Axis.Rect
4.3519975 3.6190249 3.4026665 2.9646815 2.7585392 0.1329119
R> sort(Vehicle.SAMME$importance, decreasing = TRUE)
D.Circ Max.L.Ra Max.L.Rect Pr.Axis.Ra Scat.Ra Sc.Var.Maxis
8.759478 8.373885 8.216298 7.869849 7.675569 7.190486
Comp Rad.Ra Skew.Maxis Skew.maxis Ra.Gyr Elong
6.554652 6.158310 5.712122 5.644969 4.652892 4.578929
Kurt.Maxis Kurt.maxis Circ Sc.Var.maxis Holl.Ra Pr.Axis.Rect
4.175756 4.171116 3.223761 2.969842 2.749949 1.322136
R> barplot(sort(Vehicle.bagging$importance, decreasing = TRUE),
+ main = "Variables Relative Importance", col = "lightblue",
+ horiz = TRUE, las = 1, cex.names = .6, xlim = c(0, 20))
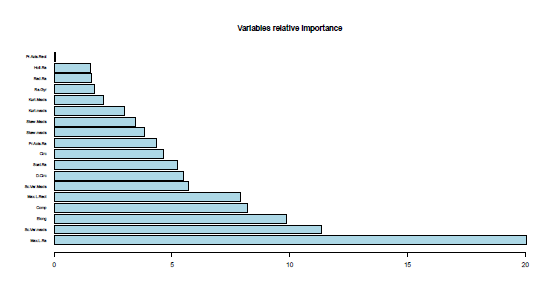 |
| Figure 9: Vehicle 데이터에서 bagging의 변수 상관 중요도. |
 |
| Figure 10: Vehicle 데이터에서 AdaBoost.M1의 변수 상관 중요도. |
 |
| Figure 11: Vehicle 데이터에서 SAMME의 변수 상관 중요도. |
Figures 12, 13 그리고 14은 이 응용(application)에서 bagging 과 boosting 분류기 마진의 누적 분포(cumulative distribution)를 보여준다. 훈련 집합의 마진은 파란색의 컬러이다 그리고 초록은 검증 집합. AdaBoost.M1에서 19.15%의 초록의 음수 마진은 검증 에러와 일치한다. SAMME에서, 파란색 선은 널 훈련 에러(null training error)이기 때문에 항상 양수이다. 그것은 bagging에서 관측의 거의 10%를 또한 강조할 수 있을 것이다, 집합 둘 모두에서, 최대 마진 1 에 이르렀다, 분류의 큰 수를 이해하게 특히 두드러짐. 요약으로 단지 앙상블의 하나를 위한 코드를 여기서 보여준다 그러나 모든 코드는 추가 파일에서 접근 가능하다.
R> margins.train <- margins(Vehicle.bagging, Vehicle[sub, ])[[1]]
R> margins.test <- margins(Vehicle.bagging.pred, Vehicle[-sub, ])[[1]]
R> plot(sort(margins.train), (1:length(margins.train)) /
+ length(margins.train), type = "l", xlim = c(-1,1),
+ main = "Margin cumulative distribution graph", xlab = "m",
+ ylab = "% observations", col = "blue3", lty = 2, lwd = 2)
R> abline(v = 0, col = "red", lty = 2, lwd = 2)
R> lines(sort(margins.test), (1:length(margins.test)) / length(margins.test),
+ type = "l", cex = .5, col = "green", lwd = 2)
R> legend("topleft", c("test", "train"), col = c("green", "blue3"),
+ lty = 1:2, lwd = 2)
 |
| Figure 12: Vehicle 데이터에서 bagging의 마진. |
 |
| Figure 13: Vehicle 데이터에서 AdaBoost.M1의 마진. |
 |
| Figure 14: Vehicle 데이터에서 SAMME의 마진. |
5. 요약 및 결론 논평 (Summary and concluding remarks)
이 논문에서, 8개의 함수를 구성하는 R 패키지 adabag를 설명했다. 이 패키지는 분류기로 CART 트리를 가지는 AdaBoost.M1, SAMME 그리고 bagging 알고리즘을 구현했다, 다중분류 작업을 처리하는 능력. 훈련된 앙상블은 제너릭(generic) predict 함수를 사용하여 새로운 데이터를 예측하기 위해 사용할 수 있다. 교차 검증 정확도 추정은 이런 분류기로 또한 이룰 수 있다. 게다가, 앙상블이 성장함에 따른 에러의 전개를 분석할 수 있다. 이것은 과적합을 찾는데 도움을 줄 수 있다 그리고, 다른 한 편으로, 만약 앙상블이 충분하게 개발되지 않았으면 계속 성장해야 한다. 전자의 경우에, 분류기를 처음부터 다시 재생성할 필요 없이 가지를 칠 수 있다, 현재 앙상블의 반복 수를 선택. 더구나, 예측된 분류가 제공될 뿐만 아니라, 그리고 모든 분류의 마진 그리고 확률의 근사값 또한 제공된다.
패키지의 주요 기능은 그들을 분류 문헌에 잘 알려진 3개의 데이터 셋을 적용하여 여기서 설명했다. 이 패키지에 구현된 3개의 알고리즘 사이의 유사점과 차이점 또한 논의했다. 마지막으로, 패키지에 여기서 사용된 약간의 plot을 추가는, 결과의 해석성을 증가하는 목적, 미래 작업의 일부분이다.

댓글 없음:
댓글 쓰기